SciPy Spatial Data

Data spasial mengacu pada data yang direpresentasikan dalam suatu ruang geometris.

Misalnya: Data yang menunjuk pada sistem koordinat.

Misalnya: menemukan apakah suatu titik berada di dalam batas atau tidak.

SciPy menyediakan modul scipy.spatial, yang memiliki fungsi untuk bekerja pada data spasial.

Section Artikel

1 Triangulasi
2 Convex Hull
3 KDTrees
4 Matriks Jarak

Triangulasi

Triangulasi poligon adalah membagi poligon menjadi beberapa segitiga yang kemudian kita dapat menghitung luas poligon.

Triangulasi dengan titik berarti membuat segitiga yang permukaannya tersusun di mana semua titik yang diberikan berada pada setidaknya satu simpul dari segitiga manapun di permukaan.

Salah satu metode untuk menghasilkan triangulasi adalah melalui titik dengan Triangulasi Delaunay().

Contoh:
Buat triangulasi dari poin-poin berikut

import sys
import matplotlib
matplotlib.use('Agg')

import numpy as np
from scipy.spatial import Delaunay
import matplotlib.pyplot as plt

points = np.array([
  [2, 4],
  [3, 4],
  [3, 0],
  [2, 2],
  [4, 1]
])

simplices = Delaunay(points).simplices

plt.triplot(points[:, 0], points[:, 1], simplices)
plt.scatter(points[:, 0], points[:, 1], color='r')

plt.show()

plt.savefig(sys.stdout.buffer)
sys.stdout.flush()

Hasilnya:

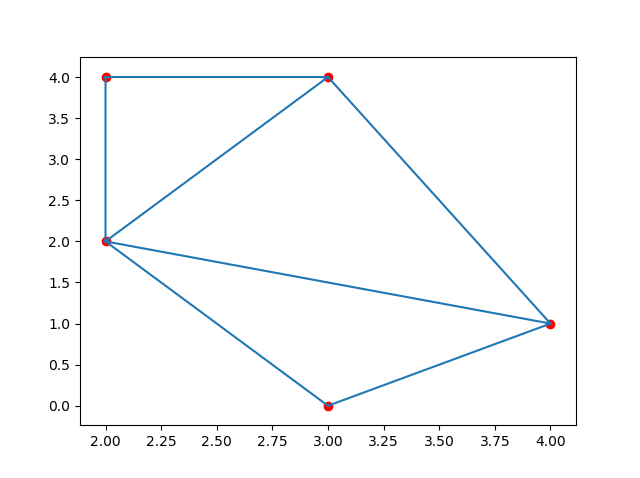
Catatan: Properti simplices membuat generalisasi dari notasi segitiga.

Convex Hull

Convex Hull adalah poligon terkecil yang menutupi semua titik yang ditentukan.

Gunakan metode ConvexHull() untuk membuat Convex Hull.

Contoh:
Buat Convex Hull untuk poin-poin berikut:

#Three lines to make our compiler able to draw:
import sys
import matplotlib
matplotlib.use('Agg')

import numpy as np
from scipy.spatial import ConvexHull
import matplotlib.pyplot as plt

points = np.array([
  [2, 4],
  [3, 4],
  [3, 0],
  [2, 2],
  [4, 1],
  [1, 2],
  [5, 0],
  [3, 1],
  [1, 2],
  [0, 2]
])

hull = ConvexHull(points)
hull_points = hull.simplices

plt.scatter(points[:,0], points[:,1])
for simplex in hull_points:
  plt.plot(points[simplex,0], points[simplex,1], 'k-')

plt.show()

#Two  lines to make our compiler able to draw:
plt.savefig(sys.stdout.buffer)
sys.stdout.flush()

Hasilnya:

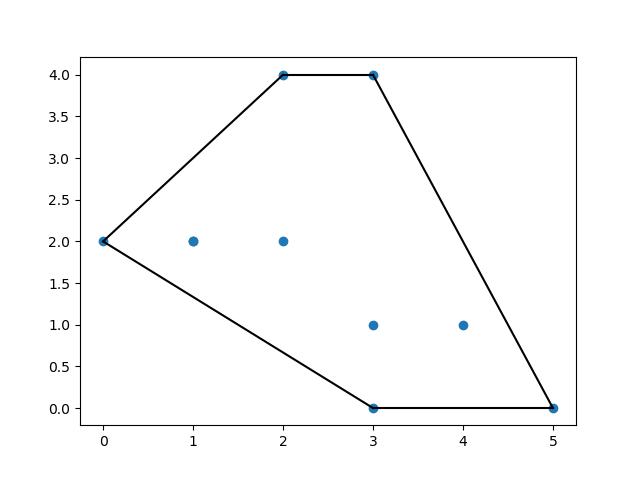
KDTrees

KDTrees adalah struktur data yang dioptimalkan untuk kueri tetangga terdekat.

Misalnya. dalam satu set poin menggunakan KDTrees kita dapat secara efisien menanyakan poin mana yang terdekat dengan poin tertentu.

Metode KDTree() mengembalikan objek KDTree.

Metode query() mengembalikan jarak ke tetangga terdekat dan lokasi tetangga.

Contoh:
Temukan tetangga terdekat ke titik (1,1)

from scipy.spatial import KDTree

points = [(1, -1), (2, 3), (-2, 3), (2, -3)]

kdtree = KDTree(points)

res = kdtree.query((1, 1))

print(res)

Matriks Jarak

Ada banyak Matrik Jarak yang digunakan untuk menemukan berbagai jenis jarak antara dua titik dalam ilmu data, jarak Euclidean, jarak kosinus, dll.

Jarak antara dua vektor mungkin tidak hanya panjang garis lurus di antara mereka, dapat juga berupa sudut di antara mereka dari asal, atau jumlah langkah satuan yang diperlukan, dll.

Banyak performa algoritme Machine Learning sangat bergantung pada matrik jarak. Misalnya. ” K Nearest Neighbors”, atau “K Means” dll.

Mari kita lihat beberapa Matrik Jarak:

Jarak Euclidean

Temukan jarak euclidean antara titik-titik yang diberikan.

Contoh:

from scipy.spatial.distance import euclidean

p1 = (1, 0)
p2 = (10, 2)

res = euclidean(p1, p2)

print(res)

Cityblock Distance (Manhattan Distance)

Apakah jarak dihitung menggunakan 4 derajat perpindahan?

Misalnya. kita hanya bisa bergerak: atas, bawah, kanan, atau kiri, tidak secara diagonal.

Contoh:
Temukan jarak cityblock antara titik-titik yang diberikan

from scipy.spatial.distance import cityblock

p1 = (1, 0)
p2 = (10, 2)

res = cityblock(p1, p2)

print(res)

Jarak Cosine

Adalah nilai sudut cosinus antara dua titik A dan B.

Contoh:
Temukan jarak kosinus antara titik-titik yang diberikan:

from scipy.spatial.distance import cosine

p1 = (1, 0)
p2 = (10, 2)

res = cosine(p1, p2)

print(res)

Jarak Hamming

Adalah proporsi bit di mana ada dua bit berbeda.

Ini adalah cara untuk mengukur jarak pada urutan biner.

Contoh:
Temukan jarak hamming antara titik-titik yang diberikan

from scipy.spatial.distance import hamming

p1 = (True, False, True)
p2 = (False, True, True)

res = hamming(p1, p2)

print(res)

python